Hier möchte ich kurz ein paar der krassesten Erscheinungen im Netz aufzeigen um deutlich zu machen, daß es eben nicht einfach so kurz mal hingezeichnet werden kann.
Peinlich wenn man schon an der Anzahl der Dreiecke scheitert und dann zum Beispiel auch noch sein Ego mit einem Video füttert. Hier das Video dazu https://www.youtube.com/watch?v=KLxPUoaBjQ8
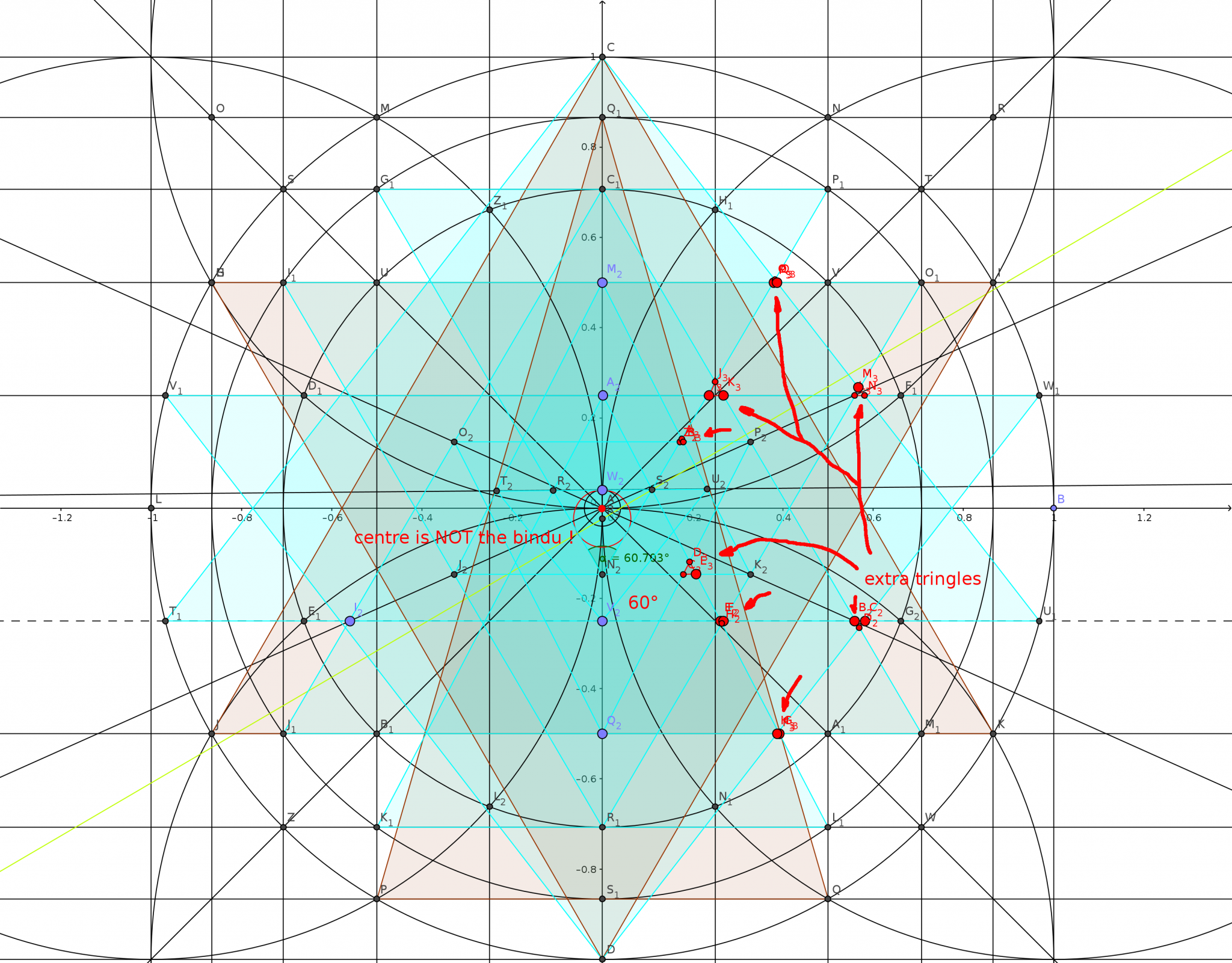
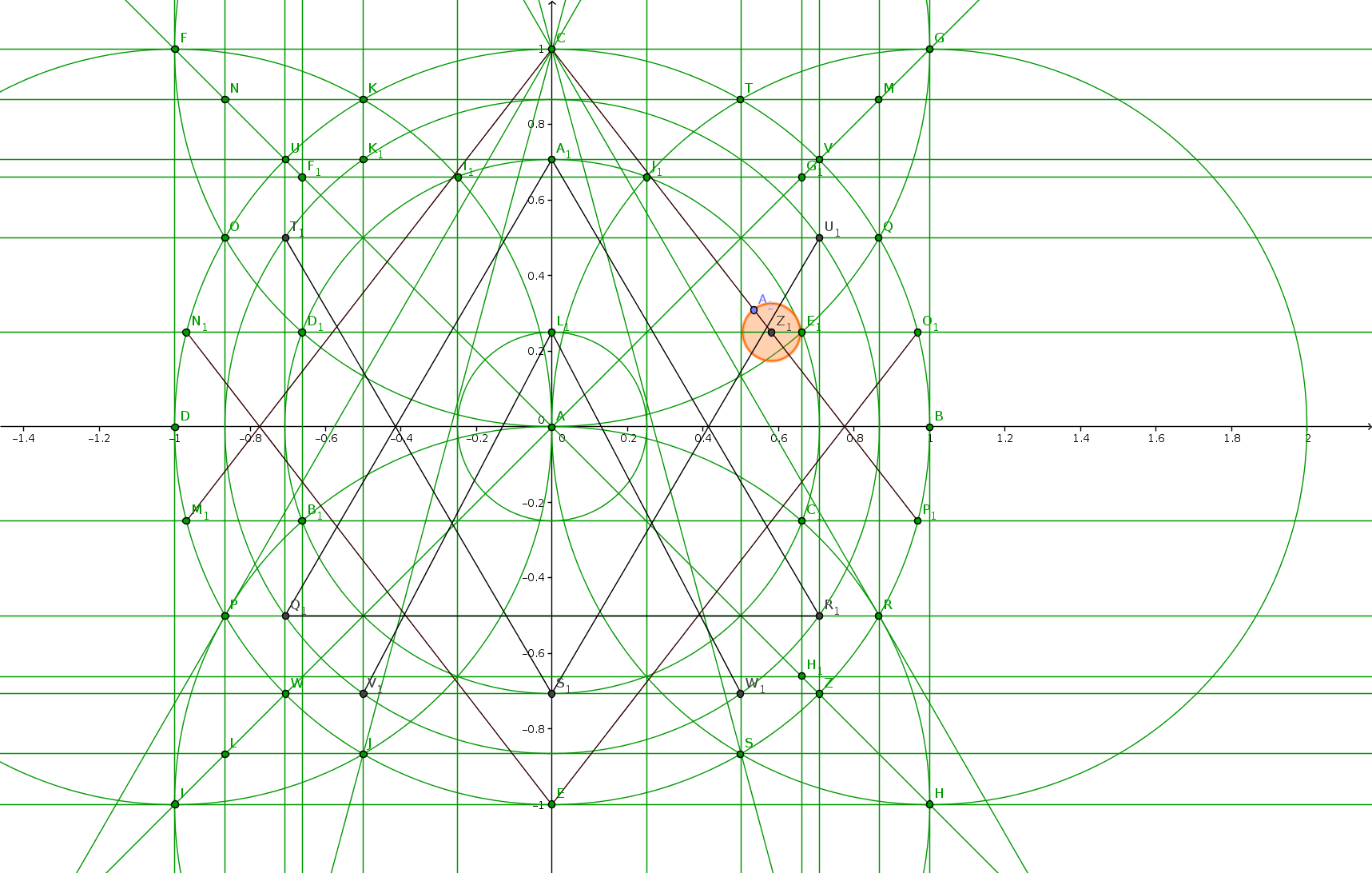
Dazu was ähnliches, wo es bei der Konstruktion schon nicht mehr weiter ging, denn welchen Schnittpunkt (roter Kreis) nehme ich zum weiter konstruieren ?
Ich kann jedem nur empfehlen ein CAD program zu benutzen um sowas zu überprüfen.
Ich nehme hier gerne das Program geogebra http://www.geogebra.org/
Ihr seht oben in dem Bild 16 extra Dreiecke, also 8 auf jeder Seite !
Der sogenannte Bindu, der Punkt in der Mitte (rot) sollte eigentlich identisch mit dem Innenkreis des inneren Dreiecks sein und dieses sollte einen Winkel von 60° haben.
Also viel mehr daneben liegen kann man fast nicht.
kurz noch
in English
I think this doesn't realy work because you get 16 extra triangles, 8 each Side AND the centre circle of the centre triangle is not the centre point of the outer circle so it is not the Bindu !! check it by your self i.e. with the program geogebra .
Nächste Fehlkonstruktion
https://www.youtube.com/watch?v=DzQ-r2A1G_w
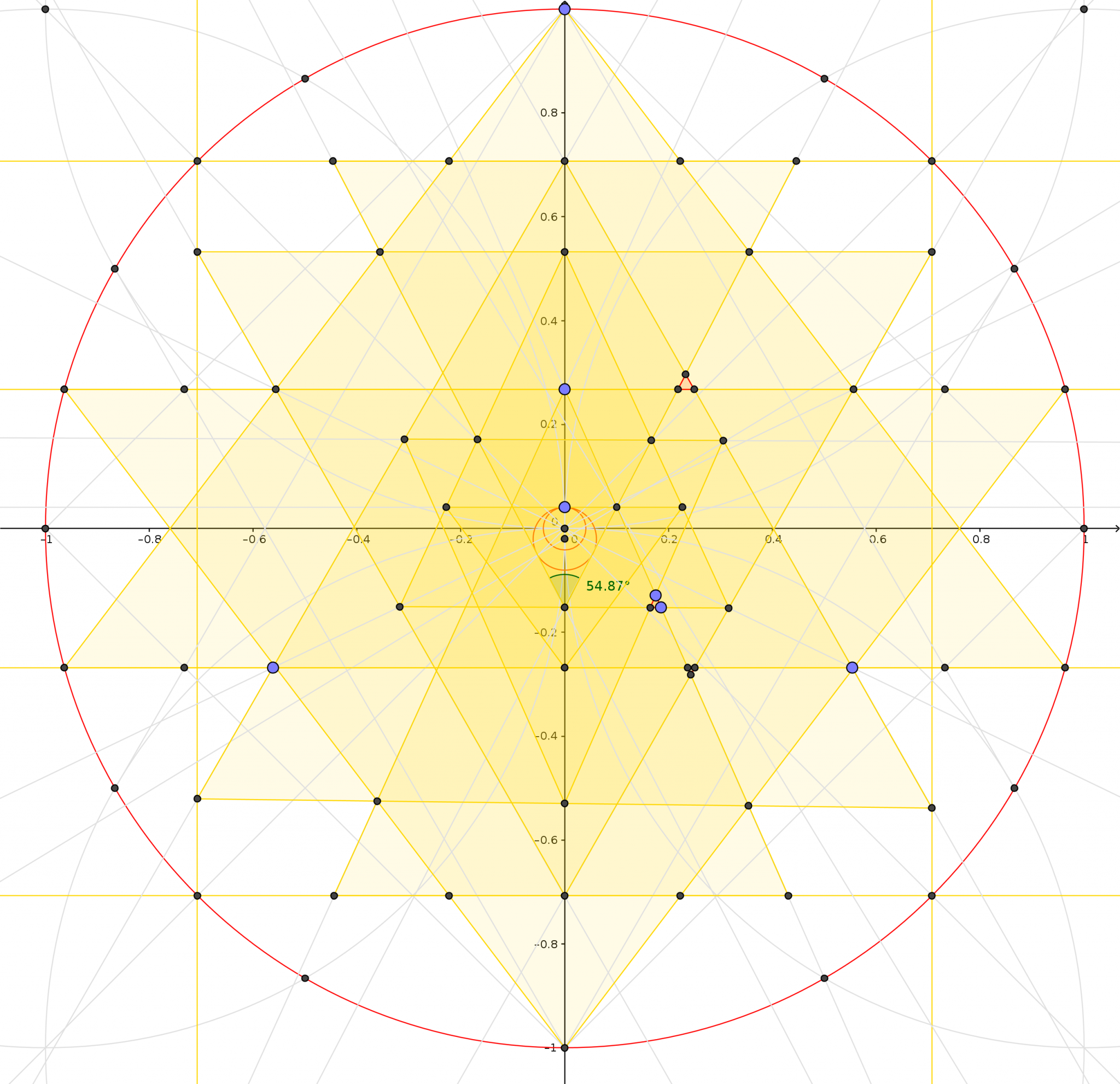
naja schon besser aber auch hier 6 Dreiecke zuviel und das Zentrum paßt auch nicht !
Noch eine weitere fehlerbehaftete Methode
https://www.youtube.com/watch?v=6olAX60szz4
Auch hier sind wieder 3 Dreiecke pro Seite, also 6 zuviel.
Und das Zentrum paßt auch nicht !
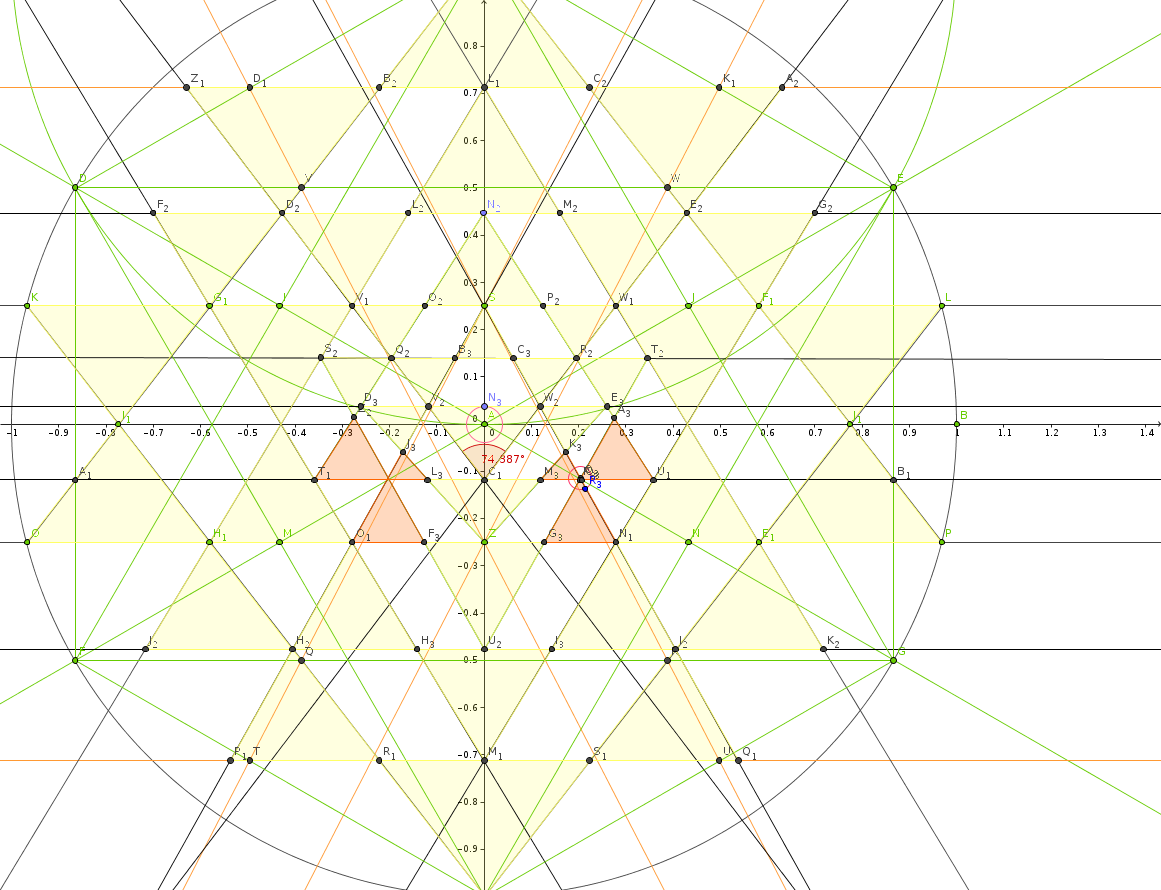
So auch hier Methode ( gefunden von Karma Ratna) sieht man sehr genau daß alle drei Grundbedingungen nicht erfüllt sind.
Weder stimmt der Winkel hier 74.387° noch das Zentrum und extra Dreiecke !
Bei dieser Methode Stimmt der Winkel mit 71,576° und der Bindu nicht
allerdings keine extra Dreiecke, was ja schon mal lobenswert ist
Vergleich mit der Methode von Achim Merath
In der Methode die ich entwickeln durfte, ist das mit den 60° zwar auch nicht ganz korrekt, aber bei 60.128° und einem Fehler des Innenkreises von 0,00218 (bei R=1) also 0,218 % zum Bindu unterhalb der Mitte kann man bei NULL extra Dreiecke sicher tollerieren.
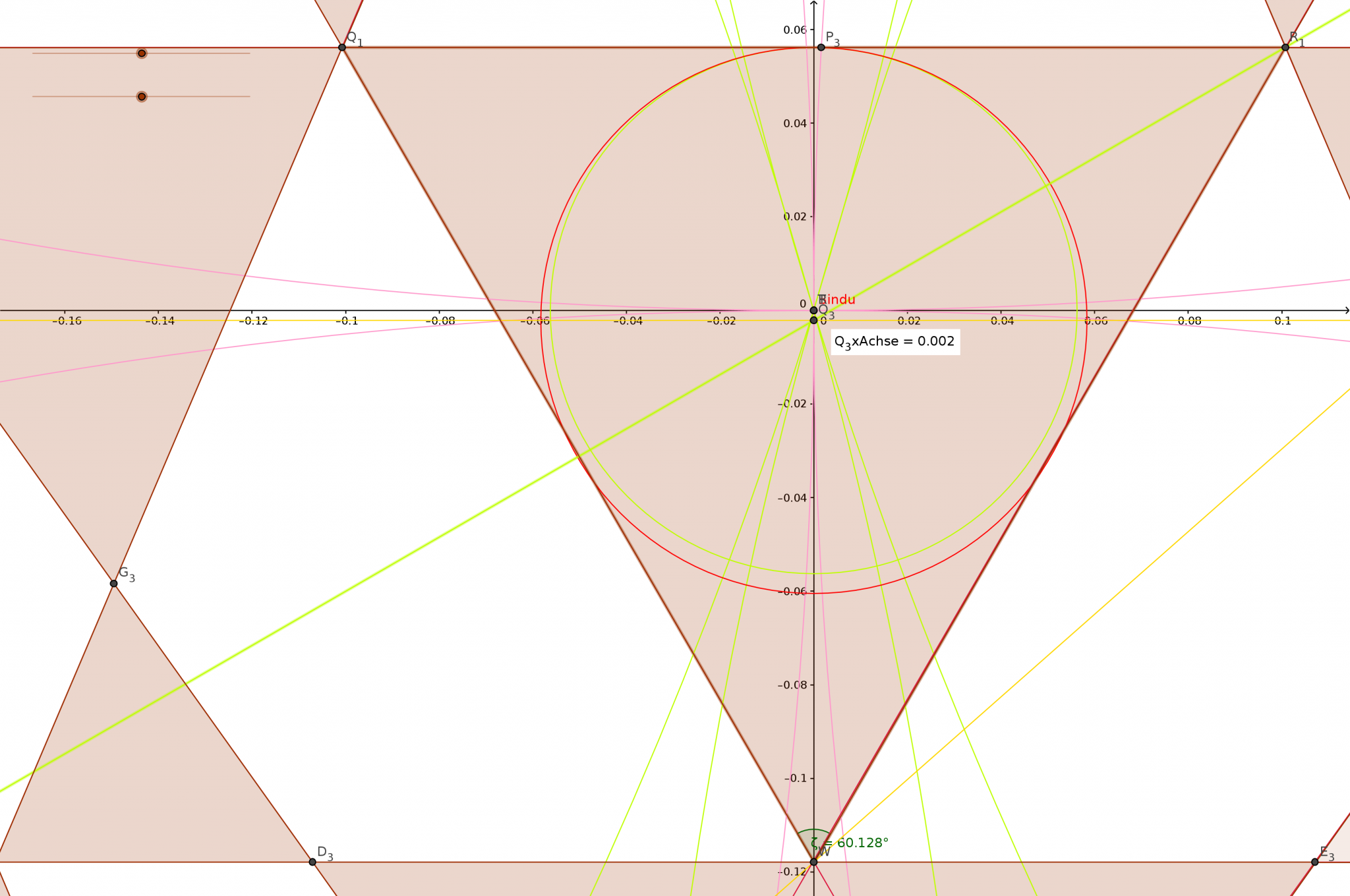
Extra Dreiecke gibt es keine !
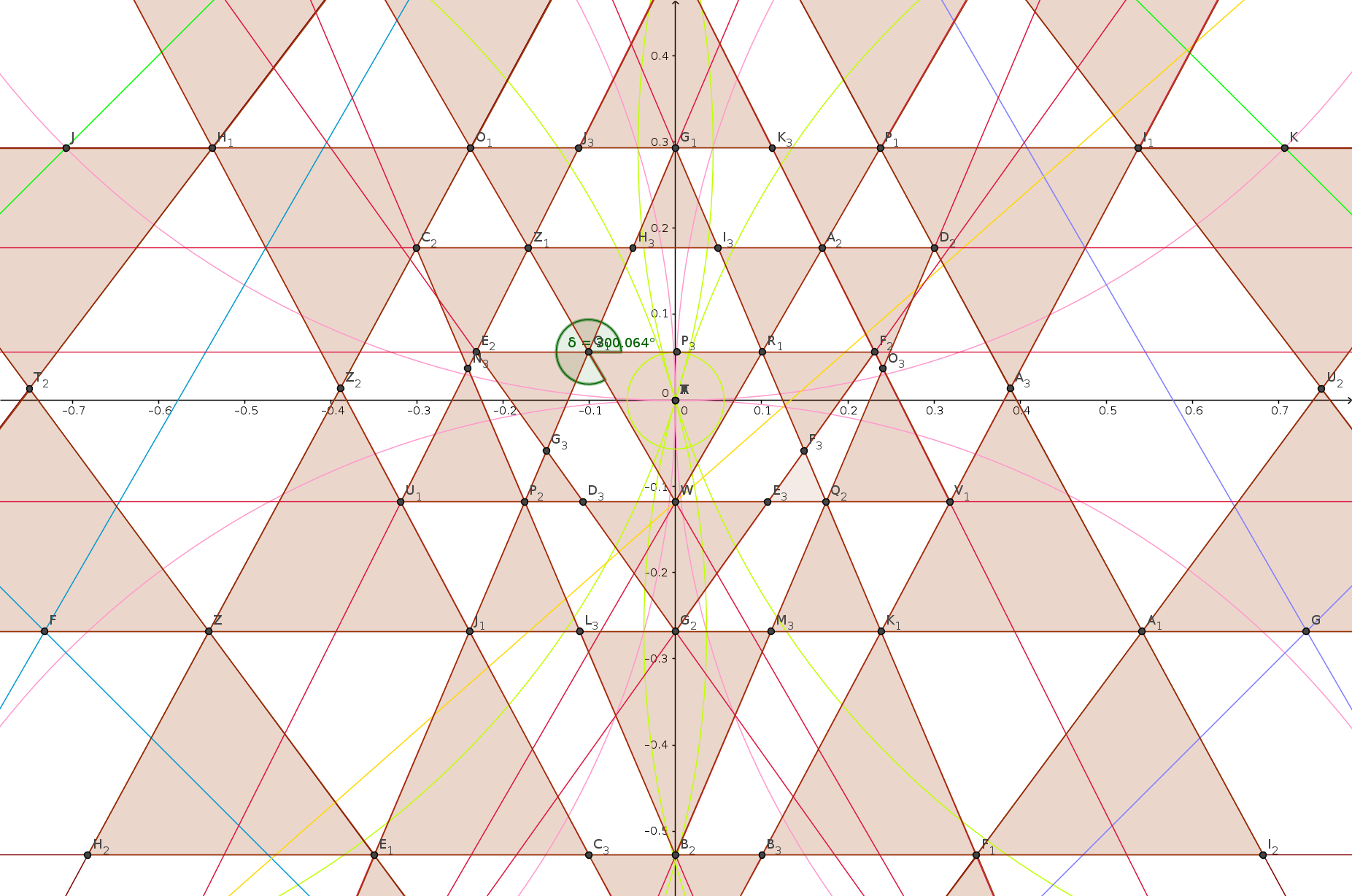
http://atelier-merath.de/sites/default/files/images/Yantra-2-4.1Par-2016...
Zum Schluß möchte ich noch kurz einige Links loswerden
http://www.sriyantraresearch.com/Optimal/optimal_sri_yantra.htm
auf dieser Seite wird das mit den 3 Kernanforderungen sehr schön erklärt. Allerdings eben auf Englisch.
